How to Write a Quantum Program for Entangling Qubits
Update 26 Mar 2024: Added answer disclosure for bonus question.
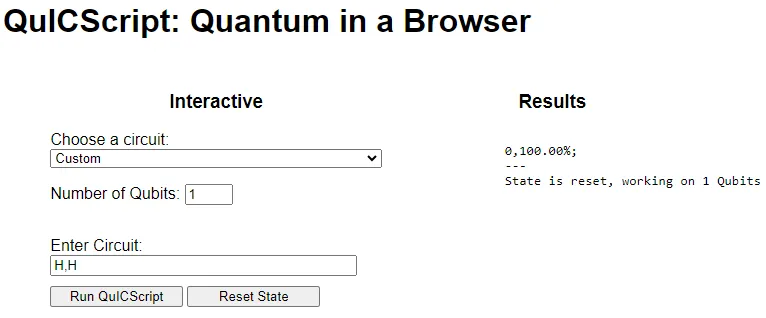
In my previous article, I shared on how to use a Hadamard gate to transform a qubit into a superposition state, resulting in the creation of a QRNG quantum program. I also posed a bonus question at the end of the article, and the answer in QuICScript is
bash
H,HIn this article, I will introduce how to transform two qubits to become quantum entangled with each other and create a quantum program to produce an output known as a Bell state. I will use |0⟩ to refer to the logical 0 state of a qubit and use |1⟩ to refer to the logical 1 state of a qubit.
Quantum Entanglement: Automation in Qubit Correlation
In (my) computing terms, quantum entanglement results in a state when two or more qubits become connected in a way that the measurement of one qubit is always results in a consistent correlation with measurements of the other qubits in the same entangled group.
An intriguing observation in quantum physics is that, regardless of the separation distance between entangled qubits, making a measurement of any qubit within the group always results in a consistent correlation among them.
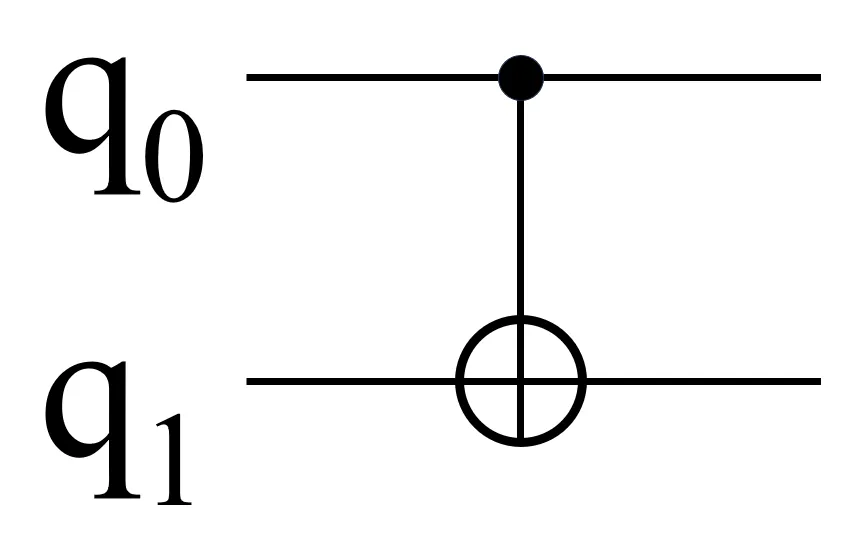
In quantum programming, entanglement of two qubits can be achieved using a Hadamard gate (H) and a controlled NOT gate (CNOT).
Function of a CNOT Gate
A Controlled-NOT gate (CNOT) is a quantum gate that operates on two qubits (namely control qubit and target qubit) and flips the state of the target qubit if the control qubit is in the |1⟩ state. If the control qubit is in the |0⟩ state, the state of the target qubit remains unchanged.
The behavior of a CNOT gate is fully described in the truth table below.
| Control Qubit (q0 Input) | Target Qubit (q1 Input) | Control Qubit (q0 Output) | Target Qubit (q1 Output) |
| |0⟩ | |0⟩ | |0⟩ | |0⟩ |
| |0⟩ | |1⟩ | |0⟩ | |1⟩ |
| |1⟩ | |0⟩ | |1⟩ | |1⟩ |
| |1⟩ | |1⟩ | |1⟩ | |0⟩ |
The Truth (Table) Behind a Pair of Quantum Entangled Qubits
Based on the truth table of the CNOT gate, you might observe that there seems to be no correlation in the output states of the control and target qubits. This is because the CNOT gate, by itself, only performs an operation on the target qubit based on the state of the control qubit. It does not directly establish correlations between the two qubits. However, if we place the control qubit into a superposition state, the output states of both qubits will become completely correlated with each other upon measurement. In other words, with the control qubit in a superposition state, the output states of both qubits become entangled as a single quantum output state. This entangled quantum state is also known as a Bell state.
An easy way to appreciate a Bell state is that the output states of both qubits will be either positively correlated or negatively correlated. The following is a truth table of a Bell state (in which we fix target qubit q1 = |0⟩ state) with positively correlated output states upon measurement.
| Qubit q0 Input | Qubit q1 Input | Qubit q0 Output | Qubit q1 Output | Probability on Measurement |
| |0⟩ or |1⟩ | |0⟩ | |0⟩ | |0⟩ | 50% |
| |0⟩ or |1⟩ | |0⟩ | |1⟩ | |1⟩ | 50% |
In the truth table above, we observe that the input state of qubit q0 does not affect the probabilities of the results, and we also observe that the output will be either both |0⟩|0⟩ or |1⟩|1⟩ states.
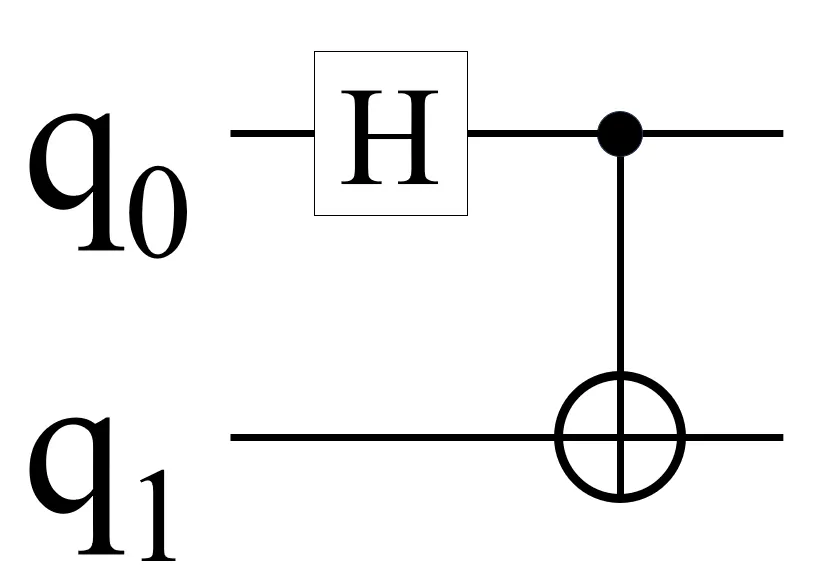
Quantum Program to Produce a Bell State
In Diagram 3 above, we connect a H gate to qubit q0, fix qubit q1 = |0⟩, and connect both qubits to a CNOT gate. The resulting output of the circuit will be a Bell state as described in the Bell state truth table earlier.
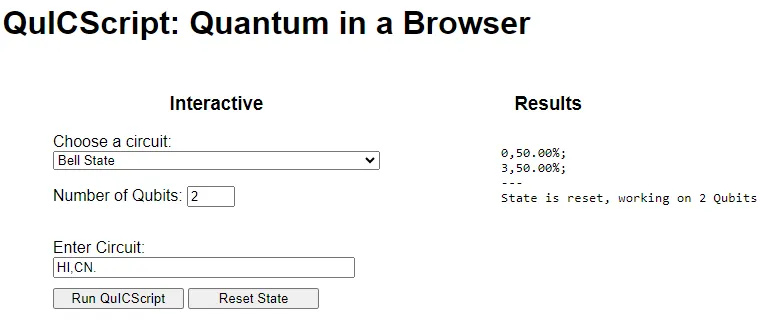
Let us verify this statistical prediction with a quantum program written in QuICScript. I will take this opportunity to introduce the Identity gate (I) which does nothing to the qubit state. In QuICScript, the Identity gate is used to indicate a passthrough connection to the next quantum gate. In QuICScript, the quantum program to produce a Bell state is as follows:
bash
HI,CNWe run the program in the Quantum-in-a-Browser to output the results shown in Diagram 4 below.
Conclusion
I hope you are pleasantly surprised, as I am, to realize how easy it is to write a quantum program to perform both quantum superposition and entanglement on two qubits to create a Bell state. If you wish to verify that changing the input state of qubit q0 does not change the measurement results of the quantum program, you may do so with the following QuICScript code. The X refers to the Pauli-X gate, which behaves as a NOT quantum gate.
bash
XI,HI,CNPS: Bonus question. What is the QuICScript program to create a Bell state with negatively correlated output states upon measurement?
See Answer
IX,HI,CNAfternote (added on 25 Mar 2024)
Some good questions have been raised by friends who read this post. I added them to this article to share these insights with everyone.
Question: Can the output qubits of the Bell circuit be used to share a random key with two parties?
Yes, these qubits can be used in this manner. Specifically, a trivial process will be to generate a pair of positively-correlated qubits via a Bell circuit, send one qubit to each of the two parties (e.g., Alice and Bob), and allow either party to measure the received qubit. Repeat the process 256 times to allow Alice and Bob to receive the same 256-bit random key to subsequently establish secure communications. However, you may notice that this trivial approach assumes the availability of a trusted channel to send the qubits to the relevant parties.
Question: What is the use of quantum entanglement in the computation aspect?
Using the Bell circuit (with positively-correlated output qubits) as a reference to facilitate understanding through visualization, quantum entanglement of the two qubits in the quantum circuit resulted, simultaneously, in the elimination of two output states (e.g., |0⟩|1⟩ and |1⟩|0⟩) and increased probabilities of the other two output states (e.g., |0⟩|0⟩ and |1⟩|1⟩). In a more general manner, quantum entanglement enables the simultaneous elimination of all invalid solutions and increased probabilities of all valid solutions before a measurement is made on the output qubits. Thus, quantum entanglement significantly reduces the computation time (as compared to classical computers) to derive valid solutions.
Author
Nicholas Ho
Nicholas seriously enjoys learning new knowledge. He is so serious about it that his hobby is to collect hobbies. His most enduring hobby, since 1997, is to continuously explore the ever-evolving domains of applied cryptography, software development, and cybersecurity. His latest aspiration is to add the word quantum in front of each of these 3 domains. Nicholas is currently a Senior Cryptographic Engineer at pQCee.com. Akin to many Singaporeans, he also enjoys collecting popular certifications, including a CS degree, an Infocomm Security masters, CISSP, and CISA.