I May Have Written the Smallest Quantum Program in the World

Update 26 Mar 2024: Added answer disclosure for bonus question.

Before delving into this article, I want to clarify that the content reflects solely my personal opinions and does not represent any official stance of the company I am associated with. Additionally, the wording of this post is intentionally crafted to aid software developers in learning quantum programming.

Why a Post on Quantum Programming?

Last week, I shared a post comparing the process of designing quantum circuits to that of designing FPGA digital circuits. Following that, several friends who read the post expressed interest in seeing a quantum program to enhance their understanding of quantum programming. Hence, in this post, I will discuss how to design a quantum random number generator (QRNG) and demonstrate its implementation using a novel quantum programming language called QuICScript. Surprisingly, a one-character QuICScript quantum program is all that's needed to specify the quantum circuit for a 1-qubit QRNG.

Background on QuICScript

QuIC stands for Quantum Interpreted Circuits, and QuICScript was developed by my CEO, Tan Teik Guan, as a hobby to streamline the process of quantum circuit development. Quantum programs written in QuICScript can be executed in real-time within a standard web browser using the Quantum-in-a-Browser engine. Currently, this engine can emulate a 20-qubit quantum computer.

I first encountered QuICScript when I joined pQCee late last year. As someone with extensive experience in software development, I was captivated by how QuICScript embodies the principles of simplicity in describing quantum circuits through its syntax and semantics. This simplicity also motivated me to prioritize learning quantum programming with QuICScript over other quantum-related programming languages. Moreover, I am eager to share the excitement I have experienced in using this new quantum programming language with others.

What is a Random Number Generator?

A random number generator (RNG) is a tool designed to produce a sequence of numbers lacking any discernible pattern or predictability. It operates by utilizing algorithms or physical processes to generate these random numbers, commonly used in various applications such as cryptography, simulations, and gaming. In essence, an RNG aims to mimic the unpredictability of natural phenomena, providing a source of randomness crucial for numerous computational tasks requiring the utmost randomness and cryptographic security.

Differences among TRNG, PRNG and QRNG

An RNG that harnesses physical processes (e.g., atmospheric noise and thermal noise) is known as a true random number generator (TRNG). Unlike pseudo-random number generators (PRNGs) that rely on deterministic algorithms, TRNGs offer truly random outputs, ensuring maximal unpredictability.

Quantum random number generators (QRNGs) leverage the inherent randomness found in quantum mechanics, utilizing phenomena like quantum entanglement or particle decay. QRNGs are purported to offer even higher levels of randomness and security by exploiting the fundamental uncertainty at the quantum level to generate truly random numbers.

Quantum Circuit Components: A Programmer-Friendly Overview

The quantum circuit generally contains two types of components. One is the qubit - a basic unit of information in quantum computing - that exhibits unique quantum properties like superposition and entanglement. The other is the quantum gate, which leverages the principles of quantum mechanics to perform operations on qubits. Together, a quantum circuit contains quantum gates that manipulate qubits to execute a quantum algorithm.

"Logical Values" in a Qubit

At a deeper technical level, a qubit is typically initialized to one of the two basis states, |0⟩ or |1⟩. Additionally, a qubit can be transformed into a superposition state, which is a linear combination of the two basis states (which mathematically means |Ψ⟩ = α|0⟩ + β|1⟩ , where |α|² + |β|² = 1). In the context of quantum programming, all qubits refer to logical qubits that are stable and reliable (i.e., immune to errors).

For our coding purposes, we can assume that the qubit can hold one of three possible states at any given time: logical 0, logical 1, and a superposition state (which can be considered an undetermined value until an asynchronous measurement operation is completed, resulting in resolution to either logical 0 or logical 1).

Function of a Hadamard Gate (H)

A Hadamard gate (H) is a quantum gate that transforms the input state of a single qubit into a superposition output state, with an equal probability (50%) of resolving to either a logical 0 or logical 1. It is important to note that there exist other gates capable of placing a qubit in a superposition state that resolves to logical 0 and logical 1 with different probabilities. In quantum algorithms, the Hadamard gate plays a crucial role in creating quantum interference and facilitating parallel computation. It serves as a cornerstone in algorithms such as the quantum Fourier transform and quantum search algorithms like Grover's algorithm.

Regardless of the input state of the qubit (either logical 0 or logical 1), the output will always result in a superposition state. Applying the Hadamard gate twice to a qubit reverses the output back to its original state prior to the operation.

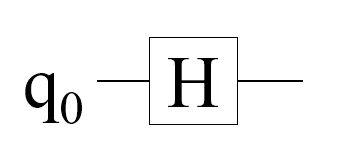
Quantum Program for a 1-qubit QRNG

In Diagram 1, we connect a qubit (q0) to a Hadamard gate (H) and connect the output to elsewhere for measurement.

Unpredictable Output of a Quantum Circuit

Recall that the output of the quantum circuit is a superposition state resulting from the Hadamard gate. This implies that upon performing a single measurement, we might observe a logical 1 as the output state. Upon resetting the quantum circuit and conducting another measurement, we might instead observe a logical 0 as the output state. If we continue resetting the quantum circuit and repeating the measurements, we will observe that the sequence of logical 0s and logical 1s is random, with no discernible pattern to predict the next measured output state.

Statistically Consistent Output of a Quantum Circuit

If we measure the output of the quantum circuit in Diagram 1 a sufficient number of times, we expect to observe logical 0 occurring with a probability of 50%, and logical 1 also occurring with a probability of 50%. This means that there is an equal likelihood of observing either state in the output, reflecting a balanced distribution between the two possible output states.

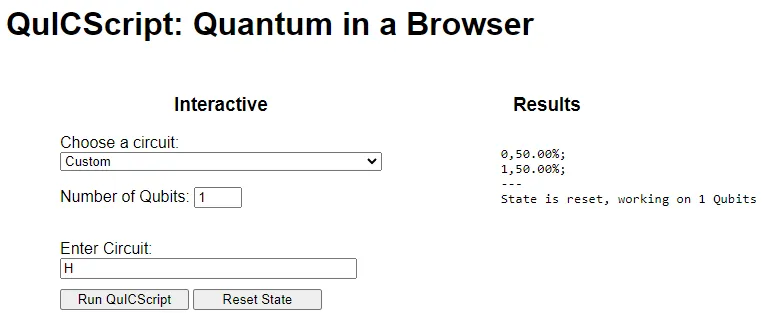
Let us verify this statistical prediction with a quantum program written in QuICScript. In QuICScript, the quantum program to specify a 1-qubit QRNG is as follows:

Yes, I kid you not! The quantum program is only one character. If we run this program in Quantum-in-a-Browser, we get the following output in Diagram 2, which contains an output result of 50% logical 0 and 50% logical 1. When you reset and run the quantum program in Quantum-in-a-Browser, the engine initializes all qubits to logical 0 before executing the program.

Desirable Properties of a QRNG

The output of the quantum program exhibited both unpredictability and a statistically consistent balanced distribution of logical 0 and logical 1. These are both desirable properties of an RNG. Thus, in theory, this quantum circuit qualifies as a 1-qubit QRNG.

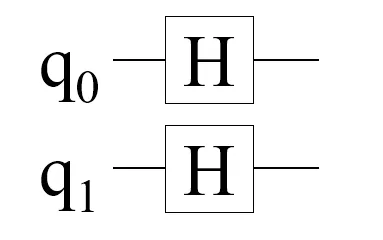
Extending to a 2-qubit QRNG

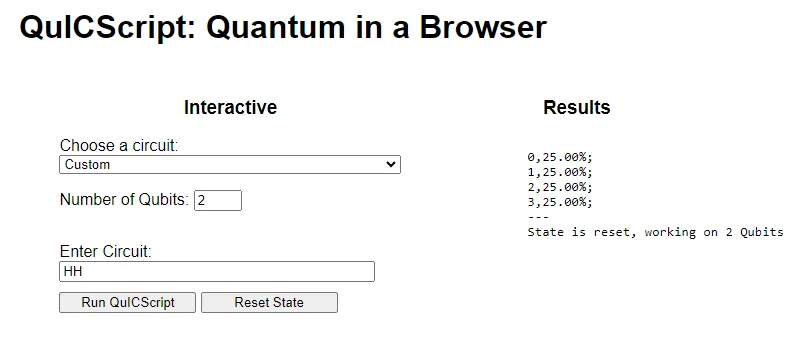
If we wish to extend the earlier quantum program to a 2-qubit QRNG, the resulting quantum circuit is shown above in Diagram 3. The QuICScript quantum program for a 2-qubit QRNG will contain 2 characters as follows:

Since there is no connection across the two qubits in the quantum circuit, the two qubits are independent of each other and result in a 25% chance for each of the four output states: logical 00, logical 01, logical 10 and logical 11. We can verify this statistical prediction against execution results from Quantum-in-a-Browser in Diagram 4.

Conclusion

The true essence of quantum computing lay not in the pursuit of certainty, but in the beauty of uncertainty itself. I hope this post empowers you to embrace the uncertainties you encounter, enabling you to take the first step in exploring a whole new world in quantum programming.

PS: Bonus question. In order to verify that applying the Hadamard gate twice to a qubit reverses the output back to its original prior state, what is the quantum program to verify this claim?  Hint: Use a comma to add gates in series along the 1-qubit quantum circuit.